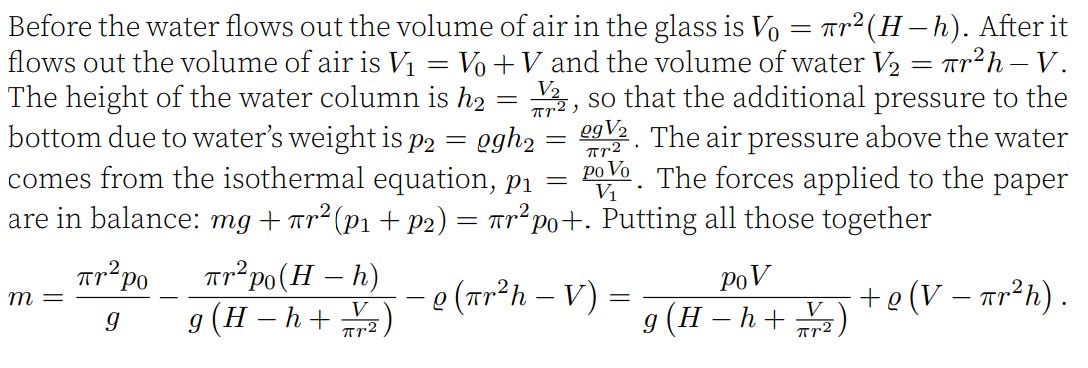I recently served as a head for the physics STEMS. STEMS is an olympiad style test which Chennai Mathematical Institute conducts. As a head, I got to design a some of the questions.
Actually most of the questions as the other two heads were too ‘busy’.
But what are Olympiads? Why are they so prestigious? And how are the questions set?
PSA: Beware of Private Olympiads
If you're in South Asia(and probably elsewhere), you've probably encountered "Olympiads" by private companies like SOF and Silver Zone. While these can be fun learning experiences, they're fundamentally different from real Olympiads like IMO or IPhO.
These private competitions are commercial ventures that charge fees for participation and materials. Their questions typically focus on speed and formulas rather than deep understanding. While suitable for younger students (below Grade 6) developing basic skills, they carry little weight with universities or real Olympiad selectors.
Real Olympiads, organized by academic and government bodies (like HBCSE and IARCS in India), test creativity and advanced problem-solving. These lead to prestigious international competitions and are recognized worldwide.
By all means, use private Olympiads as practice tools in early grades. But don't mistake them for the real thing or invest too heavily in them. Beyond Grade 6, focus on authentic competitions that genuinely develop your abilities and carry academic significance.
Don't be swayed by marketing – understand what you're participating in!
All about Olympiads(in short)
Just how Olympics are for sports, Olympiads are for academics. From mathematics to linguistics, there is an olympiad for a lot of things. Countries send a team of 4-6(based on the subject) who compete by giving these extremely difficult papers.
These papers test problem-solving skills and creative thinking in various subjects, often at levels far beyond regular curricula. These contests are known for their rigor, their ability to unearth young talent, and the sheer joy of solving problems that make your brain hurt (in the best way possible).
For most nations, the pathway is a
Pre Regional exam(not in smaller nations) → Regional/Qualifying Exam → National Exam → Training Camp → Team Selection Test aka TST (some times there is a selection test to give the TST before) → Pre-Departure Camp → International Contest.
I personally never made it past the National Exam. But I did make the national in Biology, Math, Astronomy and Informatics. As they say: Jack of all and master of none…
So, why are Olympiads so prestigious? Simple. They demand not just knowledge but ingenuity. Success in Olympiads means you’ve cracked puzzles that even seasoned professionals might struggle with.
Other than that they open doors to incredible opportunities—scholarships, mentorships, and a lot more. This is the major attractor and a reason why coaching olympiad is getting more and more valuable. Some people are now trying to ‘hack’ Olympiads and make them trainable and charge a lot (> 100 USD/hr) for this training. While we can talk about this underbelly, the bottom-line is that for most people getting to national olympiad, with decent extracurriculars gets you into some really good unis.
However, most importantly, they cultivate a mindset of persistence and curiosity, which are invaluable in any field.
Now, how are these questions set? The questions must be challenging yet solvable, elegant yet unorthodox.
A good Olympiad question isn’t about testing how much you’ve memorized—it’s about whether you can take a seemingly bizarre scenario and unravel it with logic, intuition, and subject knowledge. Sometimes, you are even given pieces of cutting edge theory, and expected to make some connections.
Additionally, I personally like to have a mix of theoretical questions and quantitative treatments of practical stuff.
I also enjoy asking people to rederive less known results from cute papers.
The problems below were from category A paper, which were meant for students from class 8-11(age 13-16).
If that intrigued you, and you have a basic idea of high school physics, please stick around, review the questions, and get a glimpse into how and what of these problems are designed. Otherwise, feel free to skip the rest of the post—you’ll probably get bored.
Objective
True or False
A motion picture film is made of a falling object which shows the object accelerating downwards. Now if the film is run backwards, it will show the object accelerating downward.
Two ring magnets are put on a stick. The weight of the setup is higher when the magnets are attracting than when they are repelling.
Suppose you lived on the moon. Suppose the earth was directly over your head. Then you would never see the earth set.
At the instant water starts getting converted to vapor, energy in form of heat causes the average speed of the particles to increase instead of increasing the temperature.
The first one is based on the Galilean idea that moving upward is just the reverse of moving downward(see the gif below). This symmetry solves a lot of kinematics questions in an instant.
But notice, the gravitational acceleration is still the same!
The source of the second one was a science semminar I attended about 10 years back. At the science center. It was just after the Mangalyan launch and Indian’s had suddenly become much more intrested in science.
The speaker(whoose name I can’t recall for the life of me) had asksed which configuration will weigh more.
The answer in this case is that the weight remains the same irrespective of the mass. I think this question is easier if you don’t know physics than if you do.
As otherwise, you start thinking about the meaning of weight(force which earth exerts on you) and how a machine calculats the weight(by balencing the normal against it) and may make some misstep in this train of thought. However, a pedegogical oversight was that someone may conclude that the magnets weigh higher while repeling and still get the ‘right’ answer.
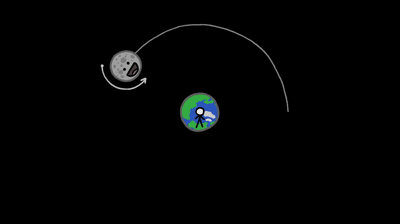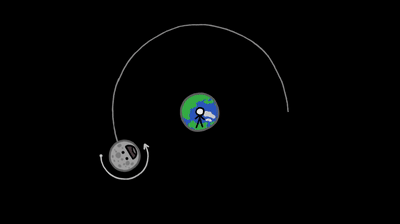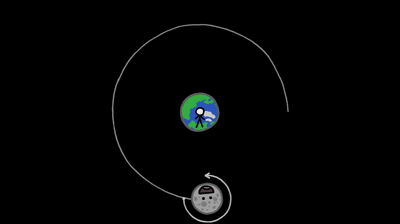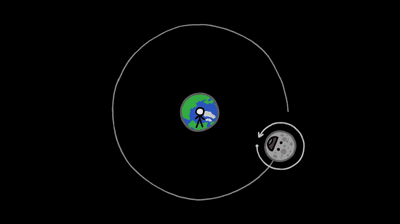
The third one is also a fact from the same seminar. If we were on moon, we would never see the earth set.
This is due to the fact that moon is tidelly locked(see gif) with respect to earth. We can litrally see only one face of the moon. We didn’t even have a cursory idea of the topology of the other face till the Chandrayan 3 mission.
This is as moon rotates, but it takes precisely as long for the Moon to spin on its axis as it does to complete its monthly orbit around Earth. Therefore, if we change our observer’s POV to the moon, we will see that earth spins in its place but its position in the sky barely changes. This can be proven concretly by the ‘gifting’ method of relative velocity. But is intutive anyways.
Thus, for moon people, there is no earth rise or earth set.
The fourth one is a very common physics error. If you prepare for JEE or NEET, it will be drilled into you that higher temprature means higher speed. This is true for ideal gases but notice, the question is not about an ideal gas or even a gas, it is about water.
The chemical structure of water differs in Ice, Water and Steam.
Imagine the molecules in ice as members of tightly organized crime syndicates. In water, they break off into smaller, looser gangs, but they're still under the thumb of some control. In steam, the molecules are like law-abiding citizens—free and moving independently.
Heating the substance is like the government enforcing stricter laws. At first, the criminals (the molecules) respond by getting faster and more frantic, trying to evade the law. But when things heat up enough, a tipping point is reached—it's like the law enforcement breaking up the larger crime families into smaller gangs. Then, when the heat increases even further, the gangs disband entirely, and the molecules are free to roam as individuals.
These tipping points—the melting and boiling points—mark moments where the added energy doesn't just speed things up. At the melting point, the heat disrupts the "syndicate" structure, turning the ice into water. At the boiling point, the energy isn't going into speeding up the molecules; it's going into breaking the last bonds holding the water together, turning it into steam.
Question Stats: 17.5 % respondents got the question correct(all four statements)
Kento had three square-shaped plane mirrors for his experiment. When he looked into one of the mirrors and squeezed his right eye, he saw a reflection as a result. Next, Kento arranged the three mirrors so that they formed three adjacent faces of a cube with a common vertex. The reflecting surfaces of the mirrors were placed on the inner side of the cube. How many reflections does Kento see?
This question is a rather simple generalization of the classic
This one is solved by a rather easy formula chart. However, the students are rarely told where these formula comes from.
We all have seen those horrer or sci-fi films where there is a mirror dimension. While such things, hopefully, don’t occur in real life. We can take the reflection of light in mirror as the same as reflection of the world in the mirror.
If we take two plane mirrors inclined at 60 degrees, we will see 5 images such that:
Extending this to 3D, we just need to see how many times we can fit a corner 8 times in a sphere. Thus, 7 of them are images.
A quantitative treatment of this will require sterdians(which is a 3D equivalent of angles) which was too complex for this paper.
Question stats: 75% of participents got this right.
Try this fun experiment: Stand at a distance and shout toward an upward flight of stairs. You might hear a chirping sound, like a bird! This happens because of the difference in frequency between the earlier and later echoes. Each step of the staircase is 12 cm high and 30 cm wide, and your distance from the lowest step is L (where L is much greater than the width and height of the stairs). Let f_h be the highest frequency and f_l be the lowest frequency produced. What is f_h - f_l in Hz, rounded to three significant figures?
This question is based on ‘How The Mound Got Its Quack’ by Felix Flicker. The accepted range of answers was 36-44 hz.
While I’ll not reproduce the entire analysis here, it is based on ‘The Mound’ in the New Collage Garden, Cambridge.
The mound is quite high, steps are quite short, thin and smooth while people are at a great distance. You will find this effect on any staircase with such a structure.
The reason this one got famous was that most people are not Oxford physicists and don’t think much about why the stairs make a strange sound when shouted at (and nor do normal people shout at stairs to begin with).
Question Stats: 1% people got it right. Others, who attempted, gave wildly wrong answers.
A fire burns at ground level releasing smoke with a temp of 40°C. The air pressure at the ground is 100 kPa and ambient temp is 20°C. Assume no heat exchange, and both smoke and air are ideal diatomic gases (molar mass = 29 g/mol). Estimate the max height the smoke can reach in meters.
This question was taken directly from Estonian-Finnish Olympiad in Physics 2008. You can find the solution here.
The question was included as it helps model a normal thing we see in a very quantitive way. Also, some small changes, will make this a much stronger model of our atmosphere. The accepted answer range is 1800-2200 m. Also, EFPhO is a wildly underated physics olympiad which I hope more people know about.
Question Stats: 10 % people got the question right. A lot of people made errors by taking R = 0.0821 J / k * Mol which is wrong in SI units but correct in different units(namely R = 0.0821 L-atm/ k * Mol). In SI units, it is 8.314 J/k*Mol.
An Edison bulb with steel filament has a power rating of 40W at 220V, and its resistance is 50Ω at room temp. Using V^2 / R, we get 968W. Given that the temperature coefficient of resistance for steel is k=0.003 per K, what is the temperature of the filament (in K) when the bulb is operating?
This question is based on an ICTS PhD interview question.
The main idea is that the temprature of the bulb’s filament is changing causing the resistence to change. This is why 50Ω is not the resistence when we use 220V power. This is a common myth propogated by school teachers(and textbooks).
The hypcrisy is that in later classes, we are told that the resistence at some later temprature is by a relation R = R0 (1 + k(T - T0)) where R0 is the resistence when the filament is at T0.
In this case, the multimeter already has told us that R0 is 50Ω at T0 = 300 K (27 C is equal to 300 K). Also, R = 1210Ω as V^2/ R = 40 W and V = 220V. Then just using the formula will give us T = 8033.3. We are accepting answers in the range 7500-8500.
Question Stats: 50% people got it right.
A water slide is 20m high, described by the equations:
x=r(θ−sinθ), h=r(1+cosθ).
The slide has two entry points: one at 20m and another at 15m. Ananya starts from the top, and Bhavana starts at 15m. Both start from rest. Let TA be Ananya's time and TB Bhavana's time.
Find TA−TB (in seconds)
This was a troll question. The function is for a shape called Tautochorme Curve. This is a special curve where from whenever you drop a ball, it takes the same time to reach the bottom.
A very interesting confusion a lot of candidates had was what do r and θ reprasent here.
r is a constant and θ is a variable. Basically, we are defining an implicit equation for the curve here.
Ex. x = f(theta); y = g(theta)
If it helps, think of it as taking a cross section of a 3-D shape. The θ helps define that shape, but in 2D, it just makes the equations neater as we don't need to get a form such that y = f(x) which may be nasty.
The analysis is based on two simple ideas, one is that we know the speed of a body at any point irrespective of the curve. This is due to the conservation of energy.
Secondly, dt = ds/v where dt is the small amount of time it takes to cover the small amount of ds and v is the velocity at that point. ds = sqrt(dx^2 + dy^2) and we can get dx and dy in terms of dθ. After that, just integrate over the required limits and you are done.
Anyways, if someone performed the analysis correctly, the answer is 0 seconds. The troll part is that most people will get confused and waste time as 0 doesn’t feel like a correct answer. How can two people start at diffrent heights but reach bottom at the same time? And this rechecking will waste time or frustrate them.
The only accepted answer is 0.
Question stats: 17.5% people answered it correctly.
Subjective Questions
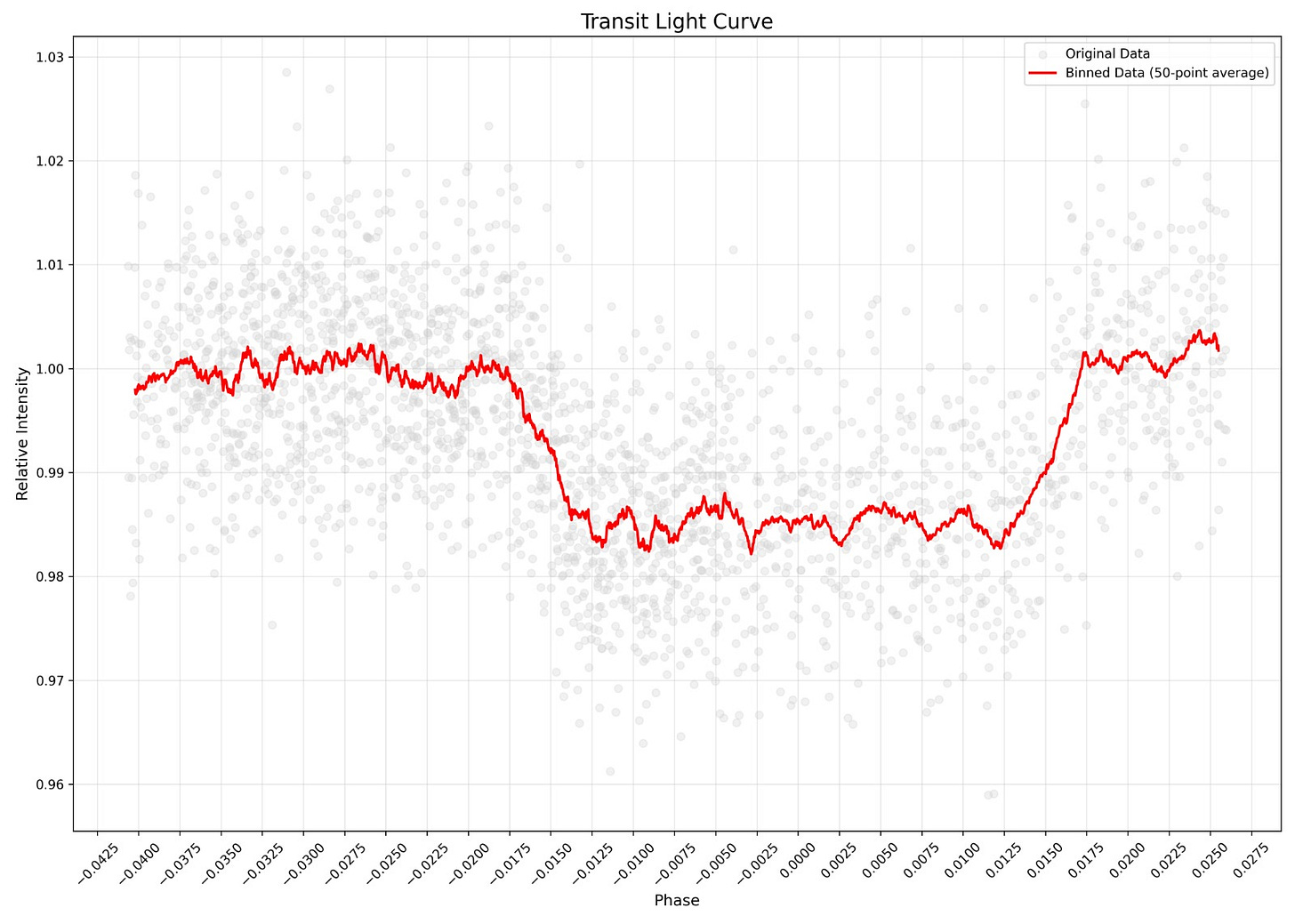
You are given a graph of relative intensity vs phase of based on a particular star in the constellation of Pegasus. Do not try to Wikipedia things as some facts have been changed.
The graph clearly indicates that the star's intensity decreases for some period. Take the orbital period to be 3.5 days and the plane of orbit to be parallel to our line of sight from Earth. Calculate the radius of planet and radius of star.
This question was based on one of the MIT OCW courses I randomly stumbled across, namely Extrasolar Planets: Physics and Detection Techniques by Dr. Sara Seager.
This question required you to understand how to google. Phases in observational astronomy go from -1 to 1. 0 is when the planet is right in the middle of the star, -1 or 1 when it is exactly opposite this.
The idea here is the that the time the planet is blocking the view to the star or the time of transit is from the start of the drop to the end of it(including the slant lines). Let this time be T. Simple geo, which follows from the figure below gives the equation
Where P is the time period the planet takes to do the full revolution of the planet, R is the radius of the star, r is the radius of the planet and a is the average radius of orbit(remember real orbits are elliptical).
a can be found using Kepler’s thrid law which relates P to a. The mass of the star can be estimated using the steller mass radius relation. This was another one of the things the candidates were required to google. The coefficient was given as 0.8.
This gives us R+r.
Now comes the other use of the graph. The difference intensity gives us flux or (r/R)^2
This will simply give us R and r.
This question was far harder than whatever was seen so far as it was worth more marks and was subjective. While the subjective checking is yet to be done, I will be surprised if the question was solved by a single candidate.
A cylindrical glass with height h and radius r was filled to a height H with water, then turned upside down with a sheet of paper covering it. The volume of water that escaped between the paper and glass was V. When the paper was released, it stayed attached, and the remaining water stayed inside. What is the maximum mass m of the paper? Given air pressure p, gravitational acceleration g, water density ρ, and that the paper is coated and does not absorb water.
This question is a quantitative formalization of this classic kids experiment. Shown in the image below. The question was borrowed from Siim Ainsaar.
The main idea is just finding all the presures and forces on the paper and balencing them. Doing it is just computation and making sure one doesn’t mess it up. Below attached is the official solution by Siim.
Each year on their Thanksgiving holiday Americans consume some 50 million turkeys. Unlike chickens, which have been bred to uniform size, turkey weights vary over an order of magnitude. Wild turkey hens weigh as little as 3 kilograms while domestic ones weigh as much as 36 kilograms. So the question arises, “How long should we cook our turkey? Last year our 9 kilogram turkey was perfect after 4 hours. This year we have a 6-kilogram turkey ?”
This question is based on an example from A Student's Guide to Dimensional Analysis by Don S. Lemons.
Dimensional analysis is a very powerful method to derive things which usually rediculed in the Indian system. Like it is covered in class 11 and then immidietly called useless and never used ever again.
On the other hand, it is one of the most powerful tools in physics. A lot of fluid mechanics runs on dimensional analysis.
This question requires a simple use of dimensional analysis. I will not bore you with the analysis. But we will get that the cooking time is propotional to M^(2/3), given the oven is the same.
Also, empirically it is known that T = M^(2/3) / 1.5. This is also called the Panofsky formula as it was first found by WKH ‘Pief’ Panosky on a thanksgiving (on what I imagine, the back of an envalope). Although, it was recently revisited in a paper titled “Physics in turkey cooking: Revisit the Panofsky formula”.
Now, one of the candidates just quoted the formula as is. I didn’t know such a formula existed. The book I got this example from, didn’t talk about it. All the AI’s I tried this question on, didn’t know.
Now I don’t know if this student is some super genius who remembers such rare results or did he just google ‘Turkey Cooking Physics’ and just copied from the abstract, not even reading the paper which turned up.
I’ll end this post with what was my personal mission statement while creating these questions and while proposing questions for the CS paper.
Science is everywhere, we just need to look closely.
We modelled smoke rising and steps chirping. Talked about how are exoplanets discovered. Quantitatively analyzed childhood experiments and even roasted a perfect turkey, all using basic physics.
I have tried, and I hope succeeded to some degree, in convincing you that physics problems are not necessarily abstract puzzles, but windows to understand our world better.
Thanks for reading,
If you enjoyed the post, click on the heart button and share the post with someone else.
If you are interested in more life, learning and science discussions, consider subscribing.
Warm Regards,
Arjun Agarwal.